引 言
隨著電子產品日益輕薄短小、元件密度愈來愈高、工作速度愈來愈快,微流控系統得到了快速發展,其中微泵在藥物微量輸送、食品和化工定量灌裝、農業育種試驗、定量噴灑藥液或水霧、電子行業精準定量點膠、集成電子元件冷卻、微量化學分析等*域得到廣泛應用。
壓電泵是一種全新驅動理論的新型微泵,它將傳統電磁泵的驅動源部分、傳動部分及泵體三者制成一體,不需附加驅動電機,具有體積小、質量輕、不受電磁干擾等優點,已成為*內外研究的熱點。1983 年荷蘭 Twente 大學將硅微加工與薄膜技術相結合研制出壓電泵
[1],韓*、德*、瑞士、美*等相繼研究開發了微型泵和微型閥
[2-19]。美*噴氣驅動實驗室利用與傳統行波馬達相似的原理為美**家航空和宇宙航行局研制出一種圓盤端面行波壓電
蠕動泵。
中*清華大學在微流量系統和微流量方面做了大量
的研究工作
[20],吉林大學研制出矩形壓電振子式主動閥壓電泵
[21-24],哈爾濱工業大學研制了壓電疊堆泵
[25],南
京航空航天大學
[26]和華南農業大學等高校都對壓電泵進行了相關的實驗和理論研究
[27],并取得了很大進展。
目前廣泛使用的
蠕動泵通常為機械
蠕動泵,主要由

收稿日期:2011-10-19 修訂日期:2012-04-05
項目基金:廣東省科技計劃項目(2010B020314003,粵科規劃字[2010]98 號)作者簡介:梁 莉(1963-),女(漢),黑龍江人,**實驗師,在讀博士生,華南農業大學工程學院,研究方向為智能農業機械,廣州 華南農業大
學工程學院自動化系,510642。Email: ll-scau@163.com
※通信作者:馬 旭(1959-),男(漢),黑龍江人,教授,博士,研究方向為農業機械化。廣州 華南農業大學工程學院農業工程系,510642。
Email: maxu1959@scau.edu.cn

泵頭、電機、泵管組成,泵頭包括轉子和泵殼,泵管置于轉子與泵殼之間,電機作為驅動器必不可少,因而增加了蠕動泵的質量和體積。
如前所述,有關壓電泵的研究主要集中于圓盤型驅動振子面外振動的壓電泵,而對于驅動振子為圓盤型面內周向行波振動的壓電蠕動泵研究則較少
[28-29]。
為此,本文將機械蠕動泵結構與壓電泵技術相結合,提出一種圓環型周向行波圓環型壓電蠕動泵,旨在進一步探索壓電技術在蠕動泵中的應用,減小蠕動泵體積和質量,簡化蠕動泵結構,進一步擴大蠕動泵的應用*域。
1 圓環型壓電蠕動泵結構及工作機理
1.1 圓環型壓電蠕動泵結構
本文設計的圓環型壓電蠕動泵結構如圖 1 所示。

1.金屬彈性體內圓環 2.壓電陶瓷片 A 區 3.壓電陶資片 B 區 4.滾柱固定
裝置 5.滾柱 6.金屬彈性體外圓環 7.硅管
圖 1 圓環型壓電蠕動泵結構圖
Fig.1 Structure of circular ring piezoelectric peristaltic pump
在金屬彈性體內、外圓環材料均為硬鋁,軸向高度
15 mm,內環外徑 38 mm,內徑 32 mm,外環內徑 42 mm,
通過之間夾有硅管,將極化并分為 A、B 區的矩形壓電陶瓷片沿金屬彈性體內圓環內側面均布粘接,其厚度為

1.2 mm,寬度 6 mm,長度 15 mm,構成了圓環復合振子,在內環外側面均布有短圓柱滾柱,為減輕質量,選用尼龍材料滾柱。
1.2 圓環型壓電蠕動泵工作原理
圓環型壓電振子以圓柱薄殼復合振子周向行波振動模態代替機械蠕動泵泵頭中的轉子擠壓硅管,省去電機驅動裝置,減少了體積和質量,工作原理如圖 2 所示。
在極化后的壓電陶瓷片 A 區和 B 區分別通以相位差為 90°、頻率和電壓幅值可調的交變電壓,由于壓電陶瓷材料的逆壓電效應,壓電陶瓷片產生交替形變,圓環型復合振子被激發出 2 個駐波,合成后在金屬彈性體外圓環產生周向行波,在周向預緊力作用下,振子沿圓周外表面行波通過尼龍滾柱不斷擠壓硅管,于是在內圓環振子外圓周與外圓環內圓環交界面上行波波峰之間就形成了多個腔體,腔體交替地形成與關閉將帶動流體沿著波的行進方向流動,管中流體受到推力,流體在此推力作用下沿圓周方向運動,實現了蠕動泵的效果。改變兩交流電壓相位差順序,流體沿圓周相反方向運動。在電壓幅值一定時,改變頻率可以控制流體的流量和壓力。其工作原理如圖 2 所示。

式(3)~(5)中,
A、B 為曲面拉梅常數;
E 為彈性模量,Pa;h 為金屬圓柱薄殼厚度,m;
ρ 為彈性體密度,kg/m
3;
g 為泊松比;
α、
β 分別為曲線坐標;
w 圓柱殼法線方向
的位移,m;
f 為圓柱殼法線方向的應力函數,Ñ
2 Ñ
2 為進行二次拉普拉斯算子運算。設
|
|
w(a , b , t ) = W (a , b )sin(wt + j) |
|
|
|
(6) |
|
|
f (a , b ,t ) = F (a , b )sin(wt + j) |
|
|
|
(7) |
|
則振型方程為 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DÑ2 Ñ 2W + Ñ 2 F - r hw2W = 0 |
|
|
|
(8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EhÑ |
2W - Ñ 2 Ñ 2 F = 0 |
|
|
|
|
|
|
|
|
|
|
(9) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對式(8)進行Ñ2 Ñ2 運算,對式(9)進行Ñ |
2 運算, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
然后相加,消去 F,可得關于 W 的 8 階齊次獨立方程 |
|
DÑ2 Ñ 2 Ñ 2 Ñ 2W + EhÑ 2 Ñ 2 FW - r hw 2 Ñ 2 Ñ 2W = 0 (10) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對于薄圓環,取柱面坐標 α=x, β=θ,其拉梅常數 A=1, |
|
B=R,主曲率半徑 Ra |
= ¥ , Rq |
= R ,則方程(10)中的算 |
|
子 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ 2 Ñ 2 = |
¶ 4 |
|
|
+ |
2 |
|
¶ 4 |
|
|
|
+ |
|
1 ¶4 |
|
|
|
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ x 4 |
|
R 2 ¶x 2 ¶q 2 |
|
R4 ¶q 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ |
2 Ñ |
2 |
|
= |
1 ¶4 |
|
|
|
|
|
|
|
|
|
|
(12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 ¶x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
對封閉薄圓環,設振型 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (x, q ) = Wn (x )cos nq |
|
|
|
(13) |
|
將式(11)、(12)、(13)代入式(10)得 |
|
|
D ( |
d 2 |
|
- |
|
n 2 |
)4W (x) + |
Eh d 4W (x) |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
dx |
|
|
|
R 2 |
R 2 |
|
|
|
dx4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
(14) |
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r hw |
( |
|
|
|
|
- |
|
|
|
|
) |
|
W (x) = 0 |
|
|
|
|
|
|
|
|
|
|
dx 2 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
設W (x ) = el x |
,代入式(14)得 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n 2 |
4 |
|
|
Eh |
|
|
4 |
|
|
|
|
|
2 |
|
|
2 |
|
n2 2 |
|
|
|
|
|
D[l |
- |
|
|
] |
|
+ |
|
R 2 |
|
l |
|
- r hw |
|
[l |
|
|
- |
|
] |
= 0 |
|
(15) |
|
|
R 2 |
|
|
|
|
|
|
|
R2 |
|
|
由式(15),得到 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
li = ± a1 , ± ia 2 , ± ( a3 |
|
+ ia4 ), ± ( a3 - ia4 ), |
|
|
|
(16) |
|
|
|
|
|
|
( j = 1, 2,3, 4,5,6,7,8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
從而可以得到 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wn (x ) = C1 sha1 x + C2 cha 1 x + C3 sina 2 x + C4 cosa2 x |
|
+ C ea 3 x sina |
x + C |
ea 3 x |
|
cosa |
x + C |
e -a3 x sina |
x |
|
|
5 |
|
|
|
4 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
7 |
|
|
|
|
4 |
|
|
|
+C e -a3 x |
cosa |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(17) |
|
8 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據薄圓環復合振子兩端的邊界條件可以建立關于待定系數
C1~
C8 的齊次線性代數方程組,由系數行列式為零,可得該復合振子的頻率方程及各階頻率與振型。
3 圓環型壓電蠕動泵的有限元分析
圓環型壓電蠕動泵是利用薄圓環復合振子在其周向

產生機械變形來擠壓膠管中的流體,薄圓環復合振子的材料特性對壓電蠕動泵的工作性能**關重要。
根據生產廠家提供的壓電陶瓷 PZT-4,各獨立特性參數值見表 1。
表 1 壓電陶瓷 PZT-4 材料特性參數表
Table 1 Material characteristic parameters table of piezoelectric ceramic PZT-4

|
參數 |
|
數值 |
|
|
|
|
|
|
C11 |
13.2 |
|
|
C12 |
7.10 |
|
彈性剛度系數 CE/ |
C13 |
7.30 |
|
(1010 N·m-2) |
C33 |
11.5 |
|
|
|
|
C44 |
2.60 |
|
|
C66 |
3.00 |
|
|
|
|
|
|
d31 |
-123 |
|
壓電常數 d/ |
d33 |
289 |
|
(10-12C·N-1) |
|
|
d15 |
496 |
|
|
|
|
|
介電常數 ε/ |
ε11 |
1475 |
|
|
|
|
(8.85×10-12 F·m-1) |
ε13 |
1300 |
|
|
|
密度 ρp/(kg·m-3) |
|
7500 |

注:
Cij(
i=1, 3, 4, 6,
j=1, 2, 3, 4 ,6)為恒電場條件下的
j 向分量變化一個單位所引起的
i 向應力分量的改變量。
金屬彈性體的內、外圓環材料皆為硬鋁,密度為 2.7 ×10
3 kg/m
3 ,硬鋁的彈性模量為 70×10
9 Pa,泊松比
g 為0.33。當壓電陶瓷參數和金屬彈性體內外圓環材料參數確定后,改變薄圓環復合振子的內、外徑及其高度等結構參數,通過對驅動振子的振動方程的分析和有限元數值計算得知,薄圓環復合振子的結構參數改變,對其諧振頻率影響較大,適當改變復合振子的結構參數,可以得到周向彎曲振動模態的振型變化如圖 3 所示,其中圖 3a 和圖 3b 分別為同型近頻振型,諧振頻率分別為 1.6815、 1.6892 kHz,模態矢量的位移相對幅值分別為 10.491 和10.506。當施加相差 90°、激勵頻率在 1.68~1.69 kHz 之
間時,將激勵復合振子產生圖 2 所示的周向行波,驅動流體產生蠕動流動。
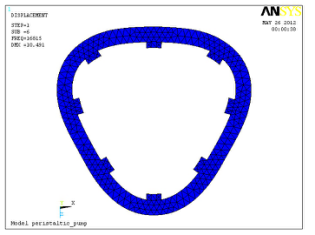
a. 驅動振子振型 1

b. 驅動振子振型 2
圖 3 驅動振子振型有限元分析
Fig.3 Finite-element analysis of vibration shape of driven stator
由此可驗證由振動方程推導出的薄圓環復合振子的振動為周向行波。
4 結 論
1)提出了一種圓環型壓電蠕動泵的新型結構,其特點是以薄圓環復合振子為驅動源;
2)由薄殼振動理論推導出該復合振子的振動方程,并可由此推導出周向行波產生的條件,對其加載相位差為 90°交變電壓所激發出的周向行波振動模態能夠實現對硅管內流體的擠壓和虹吸作用,達到蠕動效果;
3)改變交變電壓的頻率可以控制流體的流量和壓力,改變交變電壓相位順序可以改變流體流動方向,諧振頻率為可操作頻率;
4)根據有限元分析軟件優化設計出圓環型壓電蠕動泵復合振子的振型。


